Этот заголовок натолкнул меня на воспоминания о светлых временах, когда мы в школе изучали геометрию.
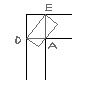
Две прямые, перпендикулярные одной и той же плоскости, параллельны.
Пока заваривал чай, сконструировал из обрывков воспоминаний доказательство. А кто-нибудь из присутствующих помнит, как это доказывается? Желательно с доказательством всех используемых теорем тоже, чтоб поинтереснее.
Школьников, которым совсем недавно учительница давала этот материал, прошу воздержаться от правильных ответов. И профильных научных сотрудников тоже. Спасибо за понимание )))
P.S. после вчерашних лучей ненависти захотелось спокойненько чего-нить обсудить.